现代扑克理论02-博奕论基础-4

最小程度剥削策略(MinES)
我们再回到通灵玩具游戏解决方案。
底池大小:100美元
筹码量:100美元
公共牌面:3♠ 3♥ 3♣ 2♦ 2♠
牌手1:EV 75美元
AA:下注100美元(100%),Check(0%)
QQ:下注100美元(50%),Check(50%)
牌手2:EV 25美元
对抗Check:用KK 100% check
对抗100美元下注:50%的时候用KK跟注,50%的时候弃牌
假设有这个游戏的一个变体,Hero是牌手1,牌手2是一个倾向于做较松跟注的对手。他不是50%的时候用KK跟注,而是55%的时候跟注。
如果Hero继续采用GTO策略,他对抗这个漏洞赚不到任何额外EV。
AA的EV:
AA下注的EV = 牌手2弃牌的EV * 牌手2弃牌率 +牌手2跟注的EV * 牌手2跟注率
AA下注的EV = 100 * 0.45 + 200 * 0.55
AA下注的EV = 45 + 110
AA下注的EV = 155美元
AA的EV = AA下注的EV * AA的下注率 + AA check的EV * AA的check率
AA的EV = 155 * 100% + 100 * 0%
AA的EV = 155美元
QQ的EV:
QQ下注的EV = 100 * 0.45 + (-100) * 0.55
QQ下注的EV = 45 + (-55)
QQ下注的EV = -10美元
QQ的EV = QQ下注的EV * QQ的下注率 + QQ check的EV * QQ的check率
QQ的EV = -10 * 50% + 0 * 50%
QQ的EV = -5
那么牌手1在这个游戏中的价值是:
牌手1的EV = AA的EV * 拿到AA的频率 + QQ的EV * 拿到QQ的频率
牌手1的EV = 155 * 50% - 5 * 50%
牌手1的EV = 50% * (155 - 5)
牌手1的EV = 75美元
这个EV和之前看到的EV相同。
如果Hero对抗这个对手执行最大程度剥削策略,他应该从不诈唬。如果他只做价值下注,他的EV将是:
AA下注的EV = 牌手2弃牌的EV * 牌手2弃牌率 +牌手2跟注的EV * 牌手2跟注率
AA下注的EV = 100 * 0.45 + 200 * 0.55
AA下注的EV = 45 + 110
AA下注的EV = 155美元
而且他从不用QQ诈唬,因此:
QQ的EV = 0
牌手1的EV = AA的EV * 拿到AA的频率 + QQ的EV * 拿到QQ的频率
牌手1的EV = 155 * 50% - 0 * 50%
牌手1的EV = 77.5美元
MES玩法相比GTO玩家每手牌多盈利2.5美元,因此在理论上Hero应该继续敲打对手。但是,从对手的角度来看,他已经看到Hero河牌圈只在50%的时候下注(而不是75%的时候),而且每次他跟注只会看到AA。Hero的假设是对手的跟注比理论上稍微松一点,并非对手是个笨蛋。即使对手非常迟钝,Hero也没有任何理由认为对手一旦意识到他从不诈唬后不会调整。
如果对手通过切换到一种总是对全压弃牌的策略来反剥削Hero,他的EV将变成:
牌手2的EV = 牌手2跟注的EV * 牌手2跟注率 + 牌手2 check的EV * 牌手2 check率
牌手2的EV = 0 * 0% + 100 * 50%
牌手2的EV = 0 * 0% + 100 * 50%
牌手2的EV = 50美元
这种策略每手牌的EV是均衡策略的两倍,反剥削的资金是Hero试图剥削资金的十倍(25 vs 2.5)!因此,在对手看懂Hero的策略并做出调整之前,Hero应该能够至少连续剥削对手10次,否则Hero将输钱。如果对手既使只在10次中反剥削Hero两次,Hero相比GTO策略仍然会输30美元,或者说每手牌多输3美元。如果对手特别迟钝,允许Hero连续45手牌剥削他,只在最后5手牌调整,那么相比简单地采用GTO玩法,Hero在这50手牌中将亏损12.5美元。
50手牌的EV = 2.5 * 45 – 25 * 5 = 112.5 – 125 = 12.5
除非对手完全忽略你的玩法,当你明显采用MES玩法并完全不平衡时,你无法指望他们忽略你的下注频率。假设他们很聪明,能够适应你的玩法,你如何用某种方式利用他们的漏洞并让自己不被他们反剥削?
你可以把他们的漏洞构建到游戏结构中。一个完美牌手的效用函数(utility function)将等于他的EV,但大多数牌手的决策会受到不同因素的影响,比如害怕输钱、害怕看起来傻、害怕被诈唬,而这些心理特征将使决策向某个方向倾斜,减少牌手的EV。
牌手1的EV:
QQ下注的QQ = 100 * (1 –C) + (-100) * C
QQ check的EV = 0
这里C是牌手2跟注的概率
牌手2的EV:
牌手2跟注的EV = AA% * 200 – QQ% * 100
这里AA%表示牌手1拿到AA的概率,QQ%表示牌手1拿到QQ的概率。
牌手2弃牌的EV = 0
在均衡情况下牌手1拿着QQ时必须对下注和check不偏不倚:
100 * (1 – C) + (-100 * C) = 0
(100 – 100C) + (-100C) = 0
100 – 200C = 0
C = 1/2
牌手2拿着KK时也应该对跟注和弃牌不偏不倚,如我们之前的证明,牌手1将总是用他的AA下注,因此:AA% = 1
那么:
QQ% * 200 – AA% * 100 = 0
QQ% = 1/2
为了把对手的漏洞构建到游戏中,我们必须从对手的角度看待游戏。在对手看来,在Hero诈唬时放弃KK是一种-EV玩法。Hero在他诈唬成功时收获X的价值。
牌手1的EV:
QQ下注的EV = (100 + X) * (1 - C) + (-100) * C
QQ check的EV = 0
牌手2的EV:
牌手2跟注的EV = QQ% * 200 – AA% * 100
牌手2弃牌的EV = -X * QQ%
我们再次应用无偏倚原则可知:
(100 + X) * (1 - C) + (-100) * C = 0
100 – 100C + X – XC – 100C = 0
-200C –XC = -X – 100
C* (200 + X) = X + 100
而且:
我们知道对手的跟注频率是55%,因此:
既然我们知道X,我们可以用它找出Hero用QQ下注的频率:
Hero在真实游戏中使用45%的QQ下注频率时他的EV是多少?
AA的EV仍然是155美元,我们需要做的只是计算QQ的EV:
QQ check的EV = 0
QQ下注的EV = -10
QQ的EV = QQ下注的EV * QQ下注率 + QQ check的EV * QQ的check率
QQ的EV = -10 * 45% + 0 * 55%
QQ的EV = -4.5
那么:
牌手1的EV = AA的EV * 拿到AA的概率 + QQ的EV * 拿到QQ的概率
牌手1的EV = 155 * 0.5 + (-4.5 * 0.5)
牌手1的EV = 77.5 – 2.25
牌手1的EV = 75.25
p93-2.jpg
表12:三种玩法的EV对比
当然,MinES玩法的EV收益不如MES玩法那么好(表12),但MinES玩法每手牌产生的0.25美元额外价值是不可剥削的,除非对手通过内在减少他的X值来弥补他的漏洞,他无法做任何事情来阻止你得到那种优势。
MinES玩法可以用现代GTO Solver软件算出,而且它不像MES玩法,你不需要知道对手的完整策略。你要做的只是假定一个特别漏洞,在Solver软件中锁定对手策略中的那个漏洞,然后试图弥补可观察到的漏洞。这样Solver软件将产生一个考虑到漏洞和对手可能做出的最好反制调整的剥削性策略。通过这样做,你将产生一个低于MES玩法的EV,同时保护自己不被反剥削。此外,MinES调整非常小,更难被对手察觉,因此你可以在他们意识到你在做什么之前长久剥削他们。最后,如果对手恢复平衡,你也必须恢复平衡,否则你将开始损失EV。
MinES策略的两个子类型
反应型MinES:这种类型的剥削只在你在真实牌局中已经发现漏洞后才调整你的策略。例如,如果你知道对手对持续下注过度弃牌(overfold),你将用均衡策略持续下注,然后调整你的转牌圈和河牌圈玩法,以适应后面回合更强的对手范围。
主动型MinES:这种类型的剥削在你的对手犯错前调整你的策略,因为你事先假定他们将犯错。例如,如果你知道对手对翻牌圈持续下注过度弃牌,你可以为了剥削这个漏洞而提高你的持续下注频率。
我建议两种MinES策略兼而有之。例如,对抗一个对翻牌圈持续下注过度弃牌的对手,你应该提高你的持续下注频率,然后,如果被跟注,就调整你的转牌圈和河牌圈玩法,因为你的范围比平常更宽,对手的范围比平常更紧。
我们在学习翻后玩法时将看到更多实例。
多人底池局面的GTO策略
纳什均衡的定义称:“没有哪个牌手可以为提高自己的期望值而单方面改变其策略。”
在任何单挑局面中,纳什均衡策略非常强大,因为这意味着采用GTO策略的牌手不可能被打败。即使你的对手知道你的确切策略,打败你在数学上也是不可能的。无论你的对手怎么做,你保证得到一个特定数目的EV。如果你采用GTO策略,而对手偏离到一种更弱的策略,他的EV只会减少,因为扑克是一种零和游戏,你将得到那部分EV。
所幸地是,纳什均衡原则不限于单挑扑克,也可应用到任何只剩两个牌手的扑克局面。
我们来看一些可以考虑单挑子博弈(subgame)的常见扑克局面:
6人桌常规局:CO玩家加注,按钮玩家3bet,盲注玩家弃牌,轮到CO玩家再次行动。牌局只剩下按钮玩家和CO玩家。
9人MTT比赛:枪口玩家加注,后面玩家弃牌,轮到大盲玩家行动。牌局只剩下枪口玩家和大盲玩家。
6人MTT比赛。劫位玩家加注,按钮玩家跟注,小盲玩家3bet,劫位玩家弃牌,轮到按钮玩家再次行动。牌局只剩下小盲玩家和按钮玩家。
太好了!GTO玩法保证你在任何只剩下两个牌手的牌局中是不可击败的,但存在三个或更多活跃牌手的扑克局面呢?
在多人底池局面中,一个牌手的错误造成的EV损失不会均等地分配给牌局中的其他牌手。在大多数场合,一些牌手能够比其他牌手利用更多错误,这取决于很多因素,比如筹码深度和位置。此外,一些牌手可能即使采用均衡策略最终也是负EV的。请考虑以下局面:
牌例
牌局类型:100美元买入网络三人Jackpot SNG比赛。
筹码量:按钮牌手12BB,小盲牌手12BB,大盲牌手12BB
牌手数量:3人(无前注)
翻前:(1.5BB)按钮玩家全压12BB,Hero在小盲位置。
小盲玩家的纳什均衡策略是用32.1%的牌全压。如果我们引入一个只用16%牌全压的鱼玩家(按钮玩家)到游戏中,我们可以使用一个全压-弃牌计算器得出各牌手的EV变化(如果两个盲注玩家继续采用纳什均衡策略或者他们调整至MES策略)。
表13:MES调整

鱼玩家偏离至较弱的策略,那当然会使他损失EV,但他的错误也使得Hero损失EV(-4.5BB/100),如果Hero继续采用GTO策略。即使Hero调整至MES策略,他仍然相比所有牌手都采用纳什均衡策略的情况每百手多损失3.2BB。
大盲玩家是这种场合的最大赢家,因为他可以获得所有额外的EV。但是,如果我们考虑后续牌局, Hero坐在大盲位置和坐在小盲位置的概率平均而言是相等的。因此,Hero也能够从鱼玩家的漏洞中获利。
总结
具有一种健全的GTO核心策略和开发一种对GTO原则的深度理解是征服现代扑克的关键,而且在艰难的牌局中至关重要。
但是,GTO并不意味着取代批判性思维。不管GTO策略有多好,牌手也应该总是注意观察对手,积极思考牌局中的每一行动。
即使在采用GTO策略保证无法打败的单挑场合,牌手们仍可以为利用对手的错误做剥削性调整。对于多人底池局面,GTO提供可用作起点的接近不可剥削的策略,但它决非最终答案也不该盲目遵循。理解和吸收GTO概念将提升你的策略,使你更难对抗,也帮助你更好地剥削对手的弱点。GTO在牌手的武器库中是一件强大的武器,但它并非唯一的武器。
每个人都应该知道的扑克数学
将底池大小定为1并使所有下注以底池大小为基准使得计算更简单。例如,如果底池有60美元而一个牌手下注20美元,他的以底池大小为基准的下注尺度是1/3底池或0.33(表14)。
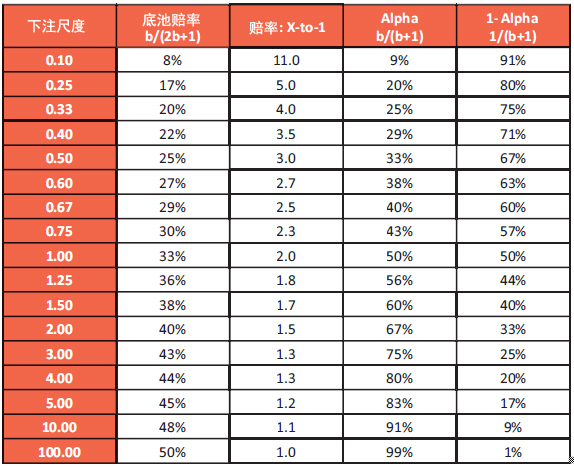
表14:下注尺度与Alpha
例子
如果你在河牌圈用两极化范围下注半个底池,你给了对手25%(3:1)的跟注赔率。你的范围应该包括75%的价值牌和25%的诈唬牌(3:1)。你的下注需要在33%(Alpha)的时候奏效才能直接获利。你的对手需要用他范围的67%(1 - Alpha)部分防守才能使你的零胜率诈唬牌对下注和check不偏不倚。

